We currently use 6 distomats to to measure the height of the platform. Using 6 non collinear measurements, you can measure the absolute position of a solid body in 3d space (3 x,y,z translations and 3 rotations of the body). If we loose one of the distomats, then the computations fails.

    The platform position is controlled by the 3 tiedown jacks/cables. These 3 jacks give us the capability to change the average height as well as tilt the platform. The ability to tilt the platform  was going to be used to correct for pitch,roll, focus errors in the feed positioning. After some testing it was realized that we did not have enough dynamic range in the jacks to correct this at all az,za positions (high za's  need lots of motion). So the tilting control was never used.

    So we have been using the distomats and tiedowns to only control the average height of the platform. When this height changes (with  temperature) we pull on all 3 tiedowns equally to move the platform vertically. You can think of the platform as a plane (triangle)  that is moving vertically. To measure the position of a plane you only need 3 non collinear points, so our 6 measurements are actually overkill. This assumes that the triangle does not undergo rotation as the temperature changes, or the weight gets redistributed (by az, dome motions).
   
  Recently some of our distomats have started to fail. They are old enough that replacements are no longer available. We've looked at replacement devices, but most of them generate too much rfi to be used (even after shielding). So we've had up to 50% of the time where we've had not measurement to control the platform height (more info).
    To solve this problem, we could  switch from trying to measure the full 3d position to just measuring the average height of the platform (with only 3 measurements).  This idea was suggested by mike nolan...

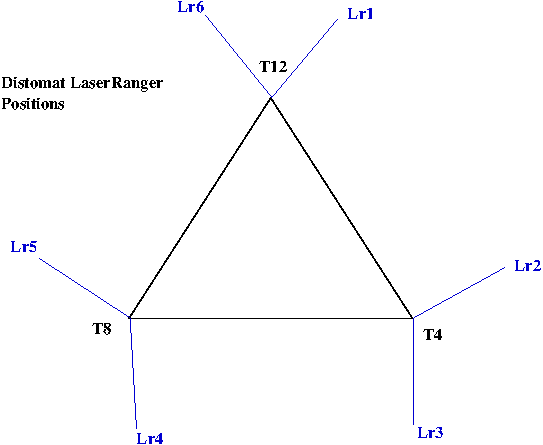
    The distomats are located about  +/- 35 degrees  from the platform corners (0,120,240).  The image below shows their positions relative to the 3 corners of the platform:

    We've got years of measurements with the 6 laser ranger distances and the computed average platform height. To compute the average platform height from 3 measurements i did the following:

• select all of the distomat measurements that had measurements from the 6 distomats.
• Compute the average length for distomats (lr1,lr3,lfr5) .. dist135
  
• Compute the average lengths for distomats (lr2,lr4,lr6).. dist246
  
• Do a linear fit to c0 + c1*dist135 = avgPlatHeight (as computed from the 6 distomat measurements)
  
• and c0 + c1*dist246=avgplatheight 
  
• The fits were done in meters..
• Data was used from:
  
• jan14-dec14
• jan15-jul15
  

2014 and 2015 using all the data.

average platform height vs 3distomat distances.

• The black points are the average length of distomats 1,3,5. The red points are the average of distomats 2,4,6
• The blue solid line is the platform height for focus.
• When the platform is in focus, the dist135 length is about 3cm longer than the dist246 length.
• there is quite a bit of scatter about the fits.

 The rotation about the z axis of the platform.

• The y axis is the z rotation
• the platform corner is  37.8 meters from the center of the triangle.
  
• A .01 degree rotation is .66 cm at the platform corner.
• The average rotation of -.018 deg is about 1.2 cm. This may be an error in the original distomat lengths used in the computation.
  
• the jumps are not necessarily motions of the platform:
  
• in 2015 it has moved .16 degrees .. this is 1.1 cm...
  
• It  may be that we are seeing:
  
•  motion of the retro reflector on the corner of the platform.
• willie did mention that one of these was not very rigid..
• It is also possible that rotating the distomat around it's focus (to maximize the signal) may actually be changing the distance.
•  i need to get the dates when the distomats were worked on to see if they correlate with the jumps.
  
• 20140311 was the date when the earthquake repairwas done.. does seem a bit of a coincidence to see  a small jump near this change.

• 20140311: jump
  
•  06 april14 .. brought down distomat to modify it..
  
• 20140423:jump
• 20140423: cleaned distomat windows, checked temperature sensors d4,d5. replaced temp sensor distomat 5.
• 20140429: cleaned and aligned the reflectors and distomats. replaced window d3 (25apr14).
• 20140826: jump
• 20140826: installed new reflector in the corner of distomat prism 6. Installed new distomat next to distomat 6 for testing. 
• 20150511:
• 20150722: jump
• 20150721 cleaned distomat windows.
• So it looks like some of the jump dates were when they were working on the distomats.
  

Fit residuals vs z axis rotation.

    The 3 distomat measurements use only 1 edge of each corner (there is a target on both sides of each vertex).

•  If the platform rotates clockwise, then the distance to distomat 1,3,5 gets shorter.
  
• This will compute to a lower platform height.

• The top frame is 2014, the bottom frame is 2015.
• Black is the distomat135 measurement, red is the distomat246 measurement.
• The equations show the actual fit values ( in meters).
  
• the residuals are highly correlated with the z rotation.
• the large scatter during 2015 dist135 is probably from distomat 5. It has been failing (up to 50% of the time). People have been working around it to try and get it to work. I wonder if it's measurement length changed because of this.
  

Histogram of fit residual

    The next plots show histograms of the fit residuals for 2014,, 2015 (.ps) (.pdf)

• The top frame is 2014 data, the bottom frame is 2015.
• the two  fits:d135,d246 have similar residuals. there were not very many zrotation jumps in 2014.
• The 2015 residuals have different distributions. this comes from the zrotation jumps during the year,.
  

Dataset with no zrotation jumps

    The data was then limited to 26aug14 thru 11may15. There were no zrotation jumps during this period.
 This dataset was then fit for avgPlatHght= c0 + c1 * avgdist3    (where avgdist3 was taken from dist135 and then dist246 measurements).

    The  plots show the results from fitting the dataset with no zrotation jumps (.ps) (.pdf)

• top frame shows the fit residuals  plotted vs zrotation angle.
• black is the d135 fit, red is the d246 fit.
  
• The fit rms is now .06 cm.
• The equations are listed.
• the bottom frame is a histogram of the fit residuals.
• they two fits now overlay each other.

• things were fine until the zrotation jump around may15, then the fit residual jumped by bout .3 cm.
  

Summary:

• We can use 3 distomat measurements to get the average platform height to within a few mm.
• The residuals  are correlated with the platform rotation in the z direction.
• The from the 26aug14 thru 11may15 (with no zrotation jumps)
  

• AvgPltHght=C0 + c1*dist135(or246)

  	C0	C1
  dist135	147.77702	1.4293739
  dist246	147.06580	1.4339539

  
  
• We've had 2 zrotation jumps in 2015. Using the above fit will cause problems:
• When the pointing changes from 6 distomats to 3 distomats there will be a jump in the computed platform height. The tiedown tracking will then move the platform by this amount. It is probably something we want to stay away from.
• We need to figure out what we are doing to cause the zrotation jumps.
  

History:

• 28aug15: installed first data set. did not remove ch away from stow when fitting
• saw jumps of .7 cm when moving from 6 distomats to dist246..
  
• 01sep15: 20:00 AST installed 2nd set of coef.. 2014 data ignoring points with ch away from stow.
  
• fit rms was .2cm .. but still saw motions of up to 2 cm moving from 6 dist to dist246
• Looks like i need to fit for the zrotation to improve the fit
• 02sep15,08:35 - turned off 3dist computation. lrMonUse3On,lrMonUse3Off() functions will turnon,off. def on boot is off.
• 03sep15: around 20:00 turned 3dist comp on. has new fit (but actually from 2015)
  
• 04sep15: around 16:00  turned 3dist comp off
  

<- page up
home_~phil