Digitizer to output: the computational pipeline

Overview of spectrometer computations:

• On the high end: Coherent signals  (sine waves, tv stations, radars, etc..). 
• On the low end: We need to keep enough bits on the the noise so that we do not add digitization noise to the signal (4 to 5 bits is probably enough).
  
• When the voltage is added (low pass filtering, butterfly stages) the sine waves increase with the number of adds (N) while the noise rms increases by the sqrt(N).
  
• A large number of "coherent" signals seen at the telescope (radars, iridium, gpsL3) are not continuous in time. If we  set the gain levels for the "on" signal, we are not guaranteed to have enough bits on the noise during the "off" time (since one goes as N and the other as sqrt(N)).
  
• The gain levels in pdev will have to be set up to give the minimum number of bits on the noise (without adding too much digitization noise). The dynamic range for the "sine waves" will then be determined by the number of bits of headroom the system has.
  

The processing stages and registers in pdev:

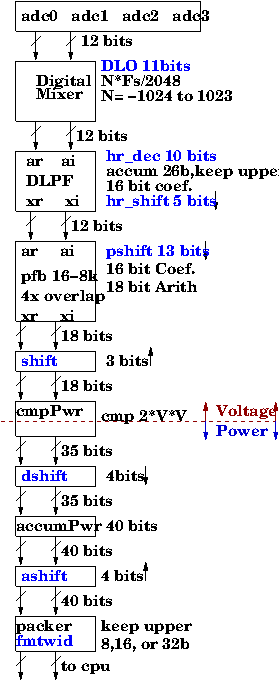
• ADC input. The converters are 12 bits.
• 
  
• DLO. The digital mixer will move N*Fs/2048 to DC. N can be -1024 to1023
• 
  
• 
  
• 
  
• 
  
• DLPF: Digital low pass filter. The accumulations are done in a 26 bit register to  avoid overflow. The output is taken from the upper most 12 bits. The DLPF  can be bypassed under program control.
  
• HR_DEC sets the decimation from 1 to 1024 (10 bit register)
  
• HR_SHIFT up shifts the accumulation before taking the upper most 12 bits. For noise, hr_shift should be set to : 10 - log2(sqrt(dec)) to keep the noise in the same bit positions prior to the DLPF.
  
• PFB: polyphase filter with 4 times overlap followed by an fft. Arithmetic is done using 18 bits. A/D 12 bits goes to upper part of 18 bits --> multiply by 64. There are log2(fftlen) butterfly stages (13 for an 8k xform).
• The pfb fir  filter adds 4 weighted numbers (spaced by fftlen). This decreases the noise rms by .75
  
• pshift is a 13 bit number. Each bit corresponds to a butterfly stage. A 1 in the bit will cause a down shift at that butterfly stage.
• 
  
• shift will upshift after the pfb (probably not needed).
• 
  
• 
  
• cmpPwr. Jeff computes 2*V*V giving 35 bits.
• 
  
• 
  
• 
  
• dshift downshifts the power before accumulating
• 
  
• 
  
• accum: accumulates in a 40 bit register
• 
  
• 
  
• ashift: 4 bit upshift of  accumulator before packing to 8,16, or 32 bits. The upper most bits are always taken.
  

Testing the gain settings:  (top)

• 32 bit mode, 8192 length spectra, integrate for .1 secs (2075 dumps). Record 10 spectra (1 second). Register settings were:
• ashift=0. Since we took the upper most 32 bits of a 40 bit register, it became a divide by 2^8=256
• number of dumps: FCNT = 2075 .  (* 8192/170e6= .1 seconds integration).
  
• dshift=0
• shift=0
• pshift=0x1555  For 13 butterfly stages we want 6.5 shifts. 0x1555 is 7 shifts.
  
• ashift=0.
  
• No decimation.
• digitizer input rms: 48 counts (measured using pnet --sigstat).
  

• page 1: spectrum of  .1 secs of data.
• top .1 second spectra. (2075 dumps summed).
  
• Mean value 43e6. Peak value around 60e6. largest 32 bit number: 4000e6.
  
• spectral shape from IF filter.
• 2nd: Normalize .1 second by 1 second average.
• Measured rms/Mean: .0213
• Expected rms/Mean: .0252
  
• scl=1.147 since we divided  .1 sec spectra by 1 sec spectra.
  
• measured/expected dif from from channel width (i assumed rectangular channels).
• Bottom: histogram of the noise (.1 second).
• .1 sec spectra flattened by 1 sec data then histogram of noise.
• page 2: Single spectrum (1 dump)
• top single spectrum
• ashift=0 --> divides by 256 when uppermost 32 bits taken from 40 bit register.
• FCNT=2075 --> divide accum spectra by  2075.
• Mean value single spectra (1 dump)=5.3e6 (scales as digRms^2).
  
• spectral rms  value  1 dump 5.8e6 (computed from chisq distribution (2 deg of freedom)).
• 2nd: spectral rms vs freq for various digitizer rms's.
• deltaT/T = 1 for a single spectra (spectral rms  = mean value).
• Multiplied mean spectral rms by bandpass shape to get channel rms vs freq.
  
• Show spectral Rms for digRms=10,20,30,48 counts (scales as digitizer rms^2).
  
• Bottom: Fraction of  Spectral channels with spectral rms < 40 cnts vs DSHIFT.
• DSHIFT downshifts spectra before accumulator. Allows us to integrate longer in the 40 bit accumulator
  
• After down shift, would like 40 counts on the noise before accumulate.
  
• The amount we can down shift depends on the mean value of the single spectra, not on how many accumulations we are going to do.
• for digRms > 20 we can down shift by 12 and still have <  3% of channels with rms < 40.
  
• page 3: Values of the voltage.
• Top: output of 8k fft. rms=1157 counts.  To compute the values:
  
•  divide single spectra  by 4 (2 since jeff computes 2*A*A and 2 because power=I^2 + q^2).
• square root to go power to voltage.
• 2nd output of PFB (input to fft). rms=1633 counts.
  
• An fft will increase a sine wave by fftlen and the rms of  the noise by sqrt(fftlen).
  
• We optionally shift or don't shift every butterfly stage. Each shift is a divide by 2.
  
• fftlen = 8192 needs 6.5 (2^6.5=sqrt(8192))  shifts to keep the noise the same amplitude.
  
•  pshift=0x1555 will shift 7 times so the fft has decreased the noise by sqrt(2)=1.4
• 3rd: input to the polyphase filter: rms=2177.
  
• I simulated the 8k hamming polyphase fir filter. The fir portion of the pfb reduced the noise rms by .75 . So 1633/.75=2177.
• Bottom: output of a/d: 34.0 .. expected: 48. error sqrt(2).
• The 12 bits of the a/d are placed in the upper 18 bits of the pfb. This multiplies the a/d value by 64.
• Computing backwards from the spectral output gives the a/d rms as 34. The measured value was 48 so we are low by sqrt(2).
  
• The sqrt(2) may be in the pwr to voltage : v=sqrt(pwr/2/2). If jeff is not computing 2*a*a then this would explain it???
  

Conclusions: (working from the digitizer input up to the spectra)   (top)

• We'd probably like to keep the rms noise counts above 32 (5 bits).
• If the LPDF is used, we should set hr_shift as 10-alog2(sqrt(dec)). Since we can only shift by 1, we could have a +/- sqrt(2) scale factor depending fractional part of on alog2(dec).
• The 12 bits of the a/d or lpdf are placed in the upper 12 bits of  the 18 bit register of the pfb. This kicks the value up by 64 so we don't have to worry too much about the pshift downshifts ending up with too few bits on the noise.
  
• the fir portion of the polyphase filter decreases the noise rms by .75 .
  
• This computation is off by sqrt(2). There is a power divide by 2 that i am including that is not really there or a voltage divide by sqrt(2) that i've included that doesn't belong.
  
• pshift should do a down shift every other butterfly. The rms will grow or decrease by sqrt(2) depending on whether we use 0x555 or 0x1555. So kick the a/d rms up by sqrt(2) if we use 0x1555.
  
• We can down shift (dshift) the spectra before accumulation by 10-12 without hurting the statistics. This will enable 32 bit 1 second integrations without having to worry about overflow.
• After changing the gain of the pfb coef. we should try long integrations with a/d rms =20,30,40,100. Normalizing to the rms=100 we should look to see where the irregularities in the spectra start as we decrease a/d rms.
  

<- page up
home_~phil